Tom M. Apostol es un matemático famoso. Cuando yo estudiaba Matemáticas era un personaje con dos caras: Una amable y motivadora, que correspondía a su libro "Cálculus" en dos tomos, escrito de manera amena y comprensible y otra frustrante y lejana, que correspondía a su libro "Análisis Matemático en Varias Variables" libro difícil donde los haya.
Más información sobre este famoso matemático fallecido en 2016, varios años después de la publicación por primera vez de esta entrada Vida y obra de Tom M. Apostol
PARA VER EXACTAMENTE ESTA MISMA ENTRADA, PERO VIENDO CORRECTAMENTE LAS FÓRMULAS SIGUE ESTE ENLACE
Años después me encuentro con una demostración suya de que la raíz de 2 es irracional. Se trata de una prueba de corte geométrico.
Ahora bien, existe una prueba clásica, que se remonta a los griegos, no sé si es la que aparece en los Elementos de Euclides, de que la diagonal del cuadrado es inconmensurable con el lado. Esa prueba figura en un montón de libros, entre ellos en el primer tomo de la Geometría Métrica de Puig Adam, publicado en 1940, aproximadamente.
A mi modo de ver la prueba nueva de Apostol es la misma que la clásica a la que me estoy refiriendo, y me sorprende que los comentaristas la traten como una novedad.
Lo que verdaderamente me sorprende es que las fuentes que citan y reproducen la demostración de Apostol no citan como precedente esa otra demostración de la inconmensurabilidad de la diagonal del cuadrado con su lado. Es más, cuando se cita un precedente, aparece el libro de texto de Kiselev, matemático ruso del siglo XIX, en la cual hay una versión de la prueba clásica de inconmensurabilidad. Pero, si no estoy equivocado, la prueba misma se remonta a la antigüedad clásica.
¡¡OJO!! La demostración aparece en un montón de autores.
Aquí enlazo un par de videos que la explican muy bien, y es interesante verlos para entender de que va todo lo que sigue, porque lo explica con mucha claridad
https://www.youtube.com/playlist?list=PLjyGOVF67WFLOSOl4FqOPBF_f81SglgBA
Te hayas enterado bien, malo regular, te lo explico en lo que sigue.
Así que se trata de una demostración muy conocida, que para Apostol "nunca existió"
Parece "la demostración que nunca existió" cuando es una demostración superconocida, que forma parte del cuerpo de teoría de geometría plana que hemos heredado desde la època de Euclides y Arquímedes.
Antes de escribir las demostraciones pongo vídeos de youtube con los dos tipos de demostraciones de la irracionalidad de $\sqrt 2 $
Demostraciones aritméticas
https://www.youtube.com/watch?v=gGWlqg-13hk
Demostraciones geométricas
En este enlace se habla sobre "conmensurable e inconmensurable", aunque ya en los vídeos de tipo geométrico ha salido explicado lo que es y la relación que tiene con la racionalidad o irracionalidad de los números
Resumiendo:
$\sqrt 2 $ es irracional
Demostraciones geométricas de este hecho.
Pueden consultarse las dos demostraciones:
La antigua, que no habla de números irracionales, sino de cantidades inconmensurables:
En la página marcada 106 del siguiente documento:
http://www.hezkuntza.ejgv.euskadi.net/r43-573/es/contenidos/informacion/dia6_sigma/es_sigma/adjuntos/sigma_33/8_solucion_eudoxo_33.pdf
La de Apostol: http://blog.plover.com/math/sqrt-2-new.html (demostración nº 7)
Por más que las comparo, sólo veo diferencias mínimas, de presentación.
En fin, que me parecen la misma demostración
Esta es la que parece que nunca existió, por más que son decenas y decenas los libros en los que aparece.
La demostración se hace por reducción al absurdo. Supongamos que la diagonal y el lado son conmensurables y llegaremos a una contradicción.
Supongamos que existe un segmento MK que divide a los segmentos AB
(cateto) y a AC (hipotenusa),
es decir: MK|AB, MK|AC.
De la geometría de la figura se deduce:
• AB = AE [radios]
• EH = HB [tangentes]
• EC = AC–AB (1)
• EH = ED [Δ(EHC) isósceles (<H=<A=<C)]
• HC = BC–BH= BC–HE = BC–EC (2)
De (1) y (2) se deduce: MK|EC, MK|HC
Hemos obtenido un nuevo triángulo isósceles, ECH, rectángulo en E, cuya hipotenusa y cuyo cateto son inferiores a la mitad de los del triángulo original y también "divisibles" por MK
Este proceso se puede reiterar indefinidamente, con el resultado de que se van obteniendo triángulos isósceles rectángulos que pueden llegar a ser "tan pequeños como se quiera", en los que el segmento fijo MK divide simultáneamente al cateto y a la hipotenusa, lo cual es manifiestamente imposible. Esto lleva a la conclusión de que no puede haber una unidad de longitud que mida simultáneamente el cateto y la hipotenusa del triángulo, es decir, estos dos segmentos no son conmensurables.
Ahora transcribo una versión de la prueba de Apostol:
Esta es una prueba totalmente brillante que √ 2 es irracional. La prueba fue descubierto por Tom M. Apostol, y fue publicado como "La irracionalidad de la raíz cuadrada de dos - una prueba geométrica" en el American Mathematical Monthly, noviembre 2000, pp 841-842.
En resumen, si √ 2 fuera racional, podríamos construir un triángulo rectángulo isósceles con lados enteros. Dado un triángulo tal, es posible construir otro que es más pequeño. Por medio de la repetición de la construcción, podríamos construir triángulos enteros arbitrariamente pequeños. Pero esto es imposible, ya que hay un límite inferior para las longitudes de los lados que un pequeño triángulo puede tener y todavía que sus lados sean enteros. Por lo tanto, no podría existir tal triángulo, en primer lugar, y √ 2 es irracional.
En detalle minucioso : Supongamos que √ 2 es racional. A continuación, mediante la ampliación del triángulo rectángulo isósceles de lados 1, 1, y 2 √ adecuadamente, se obtiene el menor posible triángulo rectángulo isósceles cuyos lados son todos los enteros. (Si √ 2 = a / b, donde a / b es en su mínima expresión (es decir, como fracción irreducible), entonces el triángulo deseado tiene lados con longitud b y una hipotenusa con longitud a.) Este es ΔOAB en el siguiente diagrama:
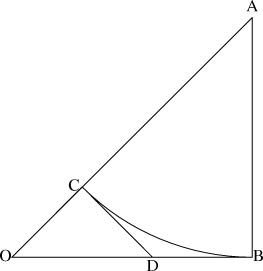
Hasta aquí la transcripción de la prueba.
Creo que la última frase del comentarista que transcribo indica que no tiene en mente la prueba clásica que he puesto en primer lugar.
¡Claro que la prueba tiene un fuerte "sabor griego"!. Es que es una versión actualizada de una prueba clásica.
Ahora colocaré una figura para comentar la demostración clásica griega de que la diagonal de un cuadrado es inconmensurable con el lado.
Otra versión de la misma figura
Se ve que es la misma figura sobre la que razonamos la demos tración de Apostol
Todo esto me lleva a pensar: ¿cuando podemos considerar nueva u original una demostración?
Aquí aparece la demostración clásica, entre otras muchas cosas
Aquí aparece la demostración de Apostol, entre otras
Una discusión del tema, aparece aquí
En este enlace aparecen varias demostraiones de la irracionalidad de raíz cuadrada de 2 (la de Apostol es la nº 7)
En esta página se expone la demostración de Apostol de manera muy clara y didáctica.
Recomiendo este documento, porque está muy trabajado y facilita enormemente la comprensión de la demostración.
Por cierto, en este documento se hace referencia a Kiselev, autor de un libro de texto que desde la década de 1890 hasta la caída de la URSS en 1990 estuvo vigente en Rusia y el resto de repúblicas de la antigua Unión Soviética. Se indica que Kiselev incluye en su libro de texto una demostración similar a la de Apostol. Ahora bien, en ningún momento el autor se atribuye la demostración, ni da pistas de que se trate de una demostración reciente, sino que por el contexto se deduce que corresponde al acervo matemático acumulado durante siglos. De esto no se comenta nada en la página de gaussianos.
Para terminar, hay que decir que la prueba de Apostol es hermosa, al igual que su precursora, y complementa al resto de pruebas que son algebraicas.
Aquí van dos pruebas, sacadas del blog "gaussianos"
La primera de ellas es la que te encuentras en casi todos los libros o artículos que tratan el tema:
Teorema: Raíz de 2 es irracional – Demostración por Reducción al Absurdo
Por tanto p2 debe ser múltiplo de 2, lo que implica que p también es un múltiplo de 2. Es decir, p = 2k para un cierto k. Sustituímos este valor de p en la expresión anterior y simplificamos un 2 de esa igualdad:
Conclusión: Raíz de 2 es irracional.
Teorema: Raíz de 2 es irracional – Demostración por Descenso Infinito
Se trata de una variante de la prueba usual, la más corriente y dice así:
Es imposible encontrar un número entero que multiplicado por sí mismo dé 2. Tampoco se puede encontrar una fracción así, pues si simplificas la fracción hasta ser irreducible, el cuadrado de esta fracción será de nuevo irreducible y por lo tanto no puede ser igual al número entero 2.
(Joseph Louis Lagrange en Lectures on Elementary Mathematics, On Arithmetic, pág 11.
Por si alguien aún no se ha enterado, se trata de una muy curiosa demostración de la irracionalidad de (y, por extensión, de la de la raíz de cualquier número natural que no sea un cuadrado perfecto).
Supongamos que no es un cuadrado perfecto y que
es racional, es decir,
con
y primos entre sí (para que la fracción sea irreducible). Lo que afirma Lagrange es que si
es irreducible (con
), entonces
también lo es. En efecto, si tenemos en cuenta la descomposición en factores primos de
y
, como
es irreducible, entonces no hay factores comunes en
y
; al elevar al cuadrado, lo que hacemos es duplicar los exponentes de los factores ya existentes, pero jamás introduciremos factores nuevos, por lo tanto,
y
tampoco compartirán factores y resultarán primos entre sí.
Y claro, si es irreducible, por mucho que queramos nunca podrá ser un número entero (recordad que
, luego, en particular,
lo que lleva a contradicción.
COMO QUERÍAMOS DEMOSTRAR
Este texto está copiado del blog Tito Eliatron Dixit y lo puedes encontrar en este enlace
Para terminar, busco completar la información que aparece profundizando en el concepto de número irracional
En mi opinión, el concepto de número irracional está muy ligado al de demostración.
Por muchas cifras decimales que hallemos, nunca podremos estar seguros de que nunca acabarán.
Es necesario demostrar que nunca se acabará
Es decir, debemos usar algún tipo de razonamiento, el simple cálculo no sirve para asegurar que un número es irracional.
Además casi siempre se trata de un tipo de razonamiento sofisticado: La demostración por reducción al absurdo. A veces se trata de demostraciones por contraposición.
En fin muchos conceptos interesantes que se pueden trabajar en estas direcciones:
http://www.uam.es/proyectosinv/estalmat/ReunionCantabria2012/Andalucia-Geometria.pdf
http://www-didactique.imag.fr/preuve/Resumes/Arsac/Arsac02.pdf
http://webdelprofesor.ula.ve/ciencias/lico/Mateducativa/demostraciones2.pdf
http://parafernaliasmatematicas.blogspot.com.es/2012/12/la-demostracion-de-apostol-de-la.html
http://cyt-ar.com.ar/cyt-ar/index.php/Courant%26Robbins_M
http://gaussianos.com/dos-demostraciones-de-la-irracionalidad-de-raiz-de-2/
http://gaussianos.com/una-demostracion-geometrica-de-la-irracionalidad-de-raiz-de-2/
http://www.youtube.com/watch?v=BLMvd3Szn7o
http://javifields.blogspot.com/2006/03/cmo-demostrar-la-irracionalidad-de-un.html
http://www.cimm.ucr.ac.cr/ciaem/articulos/educacion/concepciones/Concepciones del profesor de secundaria sobre la demostración matemática.*Vicario, Vicente y Carrillo, Jose.*Vicario,%20V.%20Cooncepciones%20del%20profesor%20de%20secundaria...2005.pdf
http://funes.uniandes.edu.co/1306/
http://grupos.emagister.com/debate/irracionalidad_de_la_raiz_cuadrada_de_2/7108-705747
Más sobre las demostraciones de la irracionalidad de $ \sqrt[]{2}$ $$\sqrt[ ]{2} $$
http://www.cut-the-knot.org/proofs/sq_root.shtml
https://foro.rinconmatematico.com/index.php?topic=8459.msg34754#msg34754
Sobre números irracionales:
http://parafernaliasmatematicas.blogspot.com.es/2014/03/numeros-irracionales.html
Bien, ya esto se acabó. Pero
como hemos hablado tanto de números irracionales, no me resisto a plantear este problema:
¿Será posible encontrar cuatro números irracionales distintos tales que su suma sea un número racional, y su producto sea 2009?
Este problema se puede encontrar aquí
Para acabar, vídeo con la demostración de que el número "pi" es irracional
https://www.youtube.com/watch?v=HmPpMreucyc
Un tema diferente, pero bastante relacionado, y desde luego bastante básico: la demostración del teorema de Pitágoras que aparece en los elementos de Euclides. Se puede consultar en eel siguiente enlace
http://vps280516.ovh.net/divulgamat15/index.php?option=com_content&view=article&id=3394%3Aeuclides-el-teorema-de-pitras-en-los-elementos-de-euclides&catid=39%3Aaso-hicieron&directory=67&showall=1
Bueno, esta fué la primera entrada
POSDATA: ALGUNAS IMAGENES



Hola, sí, en realidad parece sólo una pequeña variación la prueba de Apostol con respecto a la primer prueba que se muestra. Y en particular la idea detrás de la demostración (la esencia de la misma) en ambos casos, a mi entender, es la misma. Muy buena observación... ¡saludos!
ResponderEliminar