Un blog donde se trata la teoría de grupos es http://matematicas-de-la-simetria.blogspot.com.es/
Para aprender en condiciones teoría de grupos recomiendo http://alexmoqui.wordpress.com/
y también https://alexmoqui.wordpress.com/2012/05/22/un-curso-de-teoria-de-grupos/
Para que no te lo pierdas, lo vuelvo a recomendar al final de esta entrada
A continuación, un poco de teoría y luego problemas propuestos con pistas
http://mathdoctorbob.org/UReddit.html
Grupos de Lie
https://www.youtube.com/watch?v=4NE-KNwHKSI&list=PLAnA8FVrBl8DTFTMP8kXbDnRJHQKqfjaw
Grupos, simetrías y el teorema de Noether
https://www.youtube.com/watch?v=vnrEhb1pxeI
Los grupos de la Física
https://freelancescience.wordpress.com/2009/06/03/teoria-de-grupos-y-fisica-i-conceptos-basicos/
Curso de teoría de grupos interactivo
https://brilliant.org/courses/group-theory/
Cursos de matematicas en general
https://brilliant.org/courses/
Problemas de Geometría
http://www.analyzemath.com/geometry.html
Problemas de Cálculo
http://www.calculus.org/
Curso de álgebra abstracta en inglés, que incluye teoría de grupos:
http://matterhorn.dce.harvard.edu/engage/ui/index.html#/1999/01/82345
Vídeos sobre distintos temas matemáticos (agrupados en cursos) incluyendo algebra abstracta, teoría de grupos y análisis complejos, entre otros
https://www.youtube.com/user/MathDoctorBob/playlists
Antes de empezar, pongo un enlace a un curso de teoría de grupos, en inglés, aunque con subtítulos en inglés, lo cual lo hace más "entendible"
http://ureddit.com/class/23794/intro-to-group-theory
Otro enlace a un curso (o al menos un conjunto de videos) sobre teoría de grupos (en ingles con subtítulos en inglés)
https://www.youtube.com/watch?v=XWyyysMb-oE&list=PLWbnIo7XnOkw7zZu6u3si3at21r534qIM
Y aquí hay otro enlace a otro curso de las mismas características
https://www.youtube.com/watch?v=O4plQ5ppg9c&list=PLAvgI3H-gclb_Xy7eTIXkkKt3KlV6gk9_
Y otro más
https://www.youtube.com/watch?v=IP7nW_hKB7I&list=PLi01XoE8jYoi3SgnnGorR_XOW3IcK-
https://www.youtube.com/watch?v=IP7nW_hKB7I&list=PLi01XoE8jYoi3SgnnGorR_XOW3IcK-TP6
Y aún otros mas
https://www.youtube.com/watch?v=3wNPrSwbtQ8
https://www.youtube.com/watch?v=IP7nW_hKB7I&list=PLi01XoE8jYoi3SgnnGorR_XOW3IcK-TP6
Este es el curso que empieza con el cubo de Rubbik
cuhttps://www.youtube.com/playlist?list=PLwV-9DG53NDxU337smpTwm6sef4x-SCLv
Éste incluye algo de teoría de grupos dentro de "álgebra abstracta" que incluye toría de conjuntos y teoría de números, ambas básicas
https://www.youtube.com/watch?v=qOoQOJcjD2E&list=PLg8ZEeSiXsjgoQJzRcq60GjK0UrkMsA3-Y
Y otro enlace a curso de teoría de grupos
Y otro
https://www.youtube.com/watch?v=IP7nW_hKB7I&list=PLi01XoE8jYoi3SgnnGorR_XOW3IcK-TP6
Matemáticas superiores (introducción)
https://www.youtube.com/watch?v=CMWFmjlB8v0&list=PLZzHxk_TPOStgPtqRZ6KzmkUQBQ8TSWVX
Un grupo peculiar (muy interesante)
https://en.wikipedia.org/wiki/Modular_group#Group-theoretic_properties
Teoría de grupos para químicos (en español)
https://www.youtube.com/watch?v=wh7mIopcQ4Q
Teoría de grupos de Lie (en español)
https://www.youtube.com/watch?v=4NE-KNwHKSI&list=PLAnA8FVrBl8DTFTMP8kXbDnRJHQKqfjaw
Teorema de Wilson y teorema de Lagrange
https://www.youtube.com/watch?v=rz-GKFgowMA
https://www.youtube.com/watch?v=SUl1i8PQDZg&t=14s
Varios videos de matemáticas que incluyen algunos de teoría de grupos
https://www.youtube.com/playlist?list=PL59ADF967814E28AE
Teoria y problemas de Algebra que incluye teoría de grupos
http://fernandorevilla.es/algebra/
En realidad esta entrada viene a ser un entorno onformacional específico sobre teoría de grupos.
1) TEORÍA DE GRUPOS PRESENTADA EN DOCUMENTOS ESCRITOS Y EN VÍDEOS
No me resisto a proporcionar direcciones con información sobre teoría de grupos, la mayor parte correspondiente a los primeros cursos universitarios, y la gran mayoría en forma de documentos pdf :
http://temasmatematicos.uniandes.edu.co/Algebra_abstracta/abstracta.pdf
http://mimosa.pntic.mec.es/jgomez53/matema/docums/barrera-grupos.pdf
http://www2.uah.es/edejesus/resumenes/DECI/tema_1.pdf
http://www.virtual.unal.edu.co/cursos/ciencias/2000189_2/html/simetria-teoria-de-grupos.html
http://jrb37.mx.tripod.com/Algrebramoderna.html
http://www.instituto127.com.ar/Academicos/Catedras/ProfMate_algebra/1_Teoria_de_grupos.pdf
http://www.ugr.es/~eaznar/concepto_grupo.htm
http://bruno.stonek.com/algebra.pdf
http://simetria.dim.uchile.cl/matematico/nodo512.html
http://ibg.blogs.uv.es/
http://www.fismat.fisica.unlp.edu.ar/falomir/Notas-MF/Grupos.pdf
http://www.fismat.fisica.unlp.edu.ar/falomir/Notas-MF/Teoria-de-Grupos.pdf
http://www.fisicafundamental.net/simetrias/grupos.html
http://cms.dm.uba.ar/materias/2doCuat2007/algebra2/GRUPOSMN-2007-09-17.pdf
https://www.youtube.com/watch?v=MTHojF7OkYk&list=PL912A93B05AE44257
http://www-fp.usc.es/~edels/FM/FM-grupos.pdf
http://sociedadmatematicamexicana.org.mx/SEPA/ECMS/resumen/P1TE11_1.pdf
Y mucho más que hay en la red.
Sin embargo lo anterior me parece más que suficiente para estudiar los aspectos básicos de teoría de grupos.
2) A continuación verás algunas consideraciones sobre teoría de grupos
La teoría de grupos tiene su origen en el trabajo de E. Galois sobre solubilidad
Por lo anterior, es pertinente señalar que el término grupo
 con el orden de cualquiera de sus subgrupos. Más precisamente, afirma que si
con el orden de cualquiera de sus subgrupos. Más precisamente, afirma que si  es un grupo finito y
es un grupo finito y  es un subgrupo de
es un subgrupo de  , entonces
, entonces(1)
El recíproco del teorema de Lagrange, en general, no se cumple, pues existen grupos de orden
 que pueden no tener un subgrupo de orden
que pueden no tener un subgrupo de orden  a pesar de que
a pesar de que  . Por ejemplo, el grupo simétrico
. Por ejemplo, el grupo simétrico 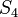 tiene orden 24 y no tiene ningún subgrupo de orden 6. En general, los grupos no resolubles son ejemplos en los que el recíproco del teorema de Lagrange no aplica.
tiene orden 24 y no tiene ningún subgrupo de orden 6. En general, los grupos no resolubles son ejemplos en los que el recíproco del teorema de Lagrange no aplica.
Estas notas están sacadas de
http://mimosa.pntic.mec.es/jgomez53/matema/docums/barrera-grupos.pdf
también de:
http://es.wikipedia.org/wiki/Teor%C3%ADa_de_grupos
también de:
http://es.wikipedia.org/wiki/Teorema_de_Lagrange_(teor%C3%ADa_de_grupos)
y de:
http://francisthemulenews.wordpress.com/2008/10/27/%C2%BFpor-que-se-utiliza-la-teoria-de-grupos-en-fisica-de-particulas-elementales/
Si embargo, la mejor manera de estudiar/repasar teoría de grupos es con los apuntes que aparecen en esta dirección, son unas notas muy buenas, claras y concisas: http://www.ugr.es/~mcarrasc/Apuntes/grupos10-11.pdf
Teoría de grupos y teoría de galois
http://matematicas-de-la-simetria.blogspot.com.es/
3) ALGUNOS PROBLEMAS RESUELTOS DE TEORÍA DE GRUPOS
(Algunos problemas están resueltos y otros con acceso a "pistas" para solucionarlos)
Con la teoría refrescada o al menos leída, pasemos a los problemas.
Antes de proponer algunos problemas, puede ser interesante practicar con problemas de los que se conoce la solución.
Esto se encuentra en la dirección http://www.matematicasypoesia.com.es/Probvarios/ProbTeoGruPreg.htm
a la cual puedes acceder pinchando aquí
Enlaces a Visual Group Theory
http://groupexplorer.sourceforge.net./
http://www.slideshare.net/sarinnae/visual-group-theory-pdf
Ahora estamos listos para intentar resolver problemas
Como voy muy apurado de tiempo dejo aquí un enlace a un problema interesante de grupos.
¡A lo mejor hay hasta respuestas!
PROBLEMA Nº1 DE ESTA ENTRADA
El problema es el siguiente:
Sea el grupo de permutaciones S(4). Dar ejemplo de dos subgrupos de orden 4. Sean J y K tales subgrupos. Determinar el menor subgrupo que contiene a ambos. ¿Es el conjunto C={ab | a pertenece a J y b pertenece a K} ese subgrupo?
Bueno, cualquier pista,
sugerencia, enlace a algún
documento o página web interesante
relacionada con el tema será
bienvenida en los comentarios.
¡Gracias de antemano, futuros
numerosos lectores!
Aquí tienes una dirección en la que puede existir alguna pista o puede que no INFORMACIÓN SOBRE EL PROBLEMA
Éste son otros problemas de teoría de grupos:
PROBLEMA Nº 2 DE ESTA ENTRADA
Si G es un grupo y
 donde
donde  es un número primo, demostrar que existen subgrupos
es un número primo, demostrar que existen subgrupos  para
para  , tales que
, tales que  , donde
, donde  es un subgrupo normal de
es un subgrupo normal de  y
y  es abeliano.
es abeliano.PROBLEMA Nº3 DE ESTA ENTRADA
Si G es un grupo con
 demostrar que
demostrar que su 7- subgrupo de Sylow es normal.
Aquí pongo otro problema, o más bien tarea de
teoría de grupos:
PROBLEMA Nº 4 DE ESTA ENTRADA
Considero el grupo diédrico
 como subgrupo del grupo de permutaciones de 4 elementos
como subgrupo del grupo de permutaciones de 4 elementos 
Sé que
 es el subgrupo generado por dos elementos a y b tales que el orden de a sea 4, el orden de b es dos y además
es el subgrupo generado por dos elementos a y b tales que el orden de a sea 4, el orden de b es dos y además  .
.Si tomo como a el 4 - ciclo
 entonces:
entonces:1.-¿Qué permutación puedo tomar como b?
2.- ¿Cómo generalizar esto a n=5, n=6... ?
3.- ¿Procedimiento para hacer lo mismo con
 y
y  ?
?Como siempre, pensadlo un poco y si queréis más información sobre el problema, la encontráis en este enlace al foro de matemáticas
Bien, ya vamos acabando.
No me apetece pasar de largo sin comentar algo
sobre una demostración no muy larga, pero en la
que siempre me equivoco.
PROBLEMA Nº5 DE ESTA ENTRADA
Un grupo es un conjunto no vacío sobre el que se ha definido una ley de composición interna que es asociativa, posee elemento neutro y elemento inverso o simétrico de cada elemento del grupo. Esto te lo dicen, de una forma u otra, todos los textos que tratan de teoría de grupos.
Algunos textos, además te dicen que en realidad no es necesario suponer unicidad de neutro ni inverso y que solo hay que suponer existencia de neutro por la izquierda (derecha) y simétrico por la izquierda (derecha)
Se trata de demostrar esto, es decir que dada una ley de composición interna asociativa en la cual existe al menos un elemento e tal que para cualquier elemento eg=g y además para cualquier elemento g existe al menos un elemento h tal que hg =e, entonces se trata de un grupo.
Usualmente la prueba se despacha en tres o cuatro líneas, y aún cuando creo haberla entendido, me lleva siempre a confusión.
Encontré un texto dónde se hacía con más detenimiento, y copio ahora un resumen de los pasos que hay que dar, en la línea de los consejos que me dan en el CASO II de esta misma entrada.
PRIMER PASO: gg=g implica g=e
SEGUNDO PASO: Si hg = e entonces gh = e
TERCER PASO: El neutro por la izquierda también es neutro por la derecha
CUARTO PASO: El elemento neutro por la izquerda es único
QUINTO PASO : Simétrico es único
SEXTO PASO: Si existe un neutro por la derecha coincide con el neutro del grupo.
SÉPTIMO PASO Si existe simétrico derecha, coincide con simétrico
Ahora se trata de seguir este esquema para realizar la demostración.
Antes de acabar, expongo una demostración diferente de este mismo hecho, encontrada en Internet:
http://memorandummatematico.wordpress.com/2012/05/17/sobre-la-definicion-de-grupo/#comment-18
http://memorandummatematico.wordpress.com/2012/05/17/sobre-la-definicion-de-grupo/
http://memorandummatematico.wordpress.com/2012/05/17/
Se trata de un blog muy interesante sobre conocimientos matemáticos y su dirección la dejo en este enlace a un interesante y bonito blog
PROBLEMA Nº 6 DE ESTA ENTRADA
1. Sea  un grupo finito en el que la unión de dos subgrupos cualesquiera es también subgrupo de
un grupo finito en el que la unión de dos subgrupos cualesquiera es también subgrupo de  . Prueba que
. Prueba que  es cíclico.
es cíclico.
2. Sea  un grupo finito en el que para cualesquiera
un grupo finito en el que para cualesquiera  subgrupos
subgrupos  o
o  . Prueba que es orden del grupo es potencia de un número primo y que el grupo es cíclico.
. Prueba que es orden del grupo es potencia de un número primo y que el grupo es cíclico.
Cuando hayas pensado lo suficiente, puedes encontrar pistas para la solución en http://rinconmatematico.com/foros/index.php?topic=64712.msg259773;topicseen#msg259773
que, para mayor comodidad pongo en este acceso a la discusión del foro de matemáticas sobre el problema
PROBLEMA Nº 7 DE ESTA ENTRADA
1. Sea  grupo y
grupo y  subgrupo de
subgrupo de  . Prueba que
. Prueba que  es normal y
es normal y  abeliano.
abeliano.
Sea  . Entonces
. Entonces 
2. Sea  grupo y
grupo y  subgrupo tal que
subgrupo tal que  , que es el centro del grupo. Prueba que
, que es el centro del grupo. Prueba que  es subgrupo normal y que si
es subgrupo normal y que si  es cíclico
es cíclico  es abeliano.
es abeliano.
Que es subrgrupo normal no hay que demostrarlo, ¿no? Creo que saldría directo de 
Y si  es cíclico, ¿de qué forma es,
es cíclico, ¿de qué forma es,  con
con  ? Tengo el mismo problema de antes, no acabo de ver cómo funcionan los grupos cocientes.
? Tengo el mismo problema de antes, no acabo de ver cómo funcionan los grupos cocientes.
Cuando lo hayas pensado un rato, puedes consultar pistas en este enlace al foro de matemáticas
PROBLEMA Nº 8 DE ESTA ENTRADA
1. Demuestra que si  es grupo finito con orden no divisible entre
es grupo finito con orden no divisible entre  , entonces para cada
, entonces para cada  existe
existe  tal que
tal que 
Sea  . Como
. Como  no es divisible por
no es divisible por  ,
,  . Por la identidad de Bézout,
. Por la identidad de Bézout,  , luego
, luego  por lo que
por lo que  . Basta tomar entonces
. Basta tomar entonces 
2. Prueba que si un grupo tiene dos elementos es abeliano, y que  es abeliano.
es abeliano.
3. Comprueba si la aplicación es o no interna
a) En  , la operación
, la operación 
b) En  , la operación
, la operación  , siendo
, siendo  al menos 5 unidades mayor que
al menos 5 unidades mayor que 
c) En  , la operación
, la operación  , siendo
, siendo  el menor entero mayor que
el menor entero mayor que  y
y 
d) División en 
e) División en 
PISTAS EN
http://rinconmatematico.com/foros/index.php?topic=64682.0
a
PROBLEMA Nº9 DE ESTA ENTRADA
Sea
G un grupo. Probar que $C^{\prime} = \{ a\in{G} \; \textrm{tales
que}\; (ax)^2 =(xa)^2 \; \textrm{para cualquier}\; x\in{G} \}$ es un
subgrupo de G
Respuesta (¿para cuando?)
En primer lugar
$C^{\prime}$
es no vacío, porque el elemento neutro pertenece a $C^{\prime}$
Supongamos que $a\in{C^{\prime}}$ entonces se cumple que $(ax)^2 =(xa)^2$ es decir $axax=xaxa$
Tomamos inversos en esa igualdad y llegamos a que
$(axax)^{-1} = (xaxa)^{-1}$ es decir que
$x^{- 1} a^{-1} x^{-1} a^{-1} = a^{-1} x^{-1} a^{-1} x^{-1}$
Como x es arbitrario, se tiene que para cualquier y tomamos
$x=y^{-1}$ y llegaremos a la conclusión de que $yaya=ayay$, es decir que $(y a^{-1})^2 = (a^{-1} y)^2$ , lo cual significa que ${ a^{-1}}\in{C^{\prime}}$
Hemos probado que todo elemento de $C^{\prime}$ tiene su inverso en $C^{\prime}$
Nos queda probar que $C^{\prime}$ es cerrado para la multiplicación del grupo
Suponiendo que $a$ y $b$ son dos elementos de
$ C^{\prime}$ entonces se cumple que
$(abx)^2 =(bxa)^2 = (xab)^2$
lo cual significa que $ab\in{C^{\prime}}$
PARA TERMINAR:
Para terminar comento este otro blog que contiene teoría de grupos, en forma de vídeos, con teoría y ejercicios, pincha para acceder a vídeos sobre grupos
Este blog ya lo he comentado en una entrada propia en este blog, titulada "un blog prometedor"
Un caso particular de grupo es el grupo simétrico. En la siguiente entrada de éste mismo blog se ofrece información sobre el mismo:
http://parafernaliasmatematicas.blogspot.com.es/2013/03/grupo-simetrico.html
SECCIÓN DE PROBLEMAS RESUELTOS DE TEORÍA DE GRUPOS
Aquí hay problemas resueltos de introducción a la teoría de grupos
Problemas resueltos de teoría de grupos
Más problemas resueltos de teoría de grupos
Acceso a problemas de teoría de grupos
Gran Traca Final: un montón de archivos sobre teoría de grupos
https://drive.google.com/folderview?id=0BzfhQuA7D_e6Y2VLaGx0QTlXVkU&usp=sharing
Para aprender no sólo teoría de grupos, sino Álgebra Abstracta en general, aquí están los siguintes enlaces:
Enlaces a cursos de álgebra abstracta
https://www.youtube.com/watch?v=aENEYDFQnfA&list=PLF379B0552AD17780
Otro curso de Álgeba Abstracta
https://www.youtube.com/watch?v=VdLhQs_y_E8&list=PLelIK3uylPMGzHBuR3hLMHrYfMqWWsmx5
Otro curso de Álgebra Abstracta
https://www.youtube.com/watch?v=N-5Av1KC11w&list=PLL0ATV5XYF8DTGAPKRPtYa4E8rOLcw88y
Y todavía un curso más sobre álgebra abstracta
https://www.youtube.com/watch?v=CMWFmjlB8v0&list=PLZzHxk_TPOStgPtqRZ6KzmkUQBQ8TSWVX
https://www.youtube.com/watch?v=IP7nW_hKB7I&list=PLi01XoE8jYoi3SgnnGorR_XOW3IcK-TP6
https://www.youtube.com/watch?v=mvmuCPvRoWQ
Un curso más de Álgebra Abstracta
https://www.youtube.com/playlist?list=PLmU0FIlJY-Mn3Pt-r5zQ_-Ar8mAnBZTf2
https://www.youtube.com/channel/UCErLELnXehsJ7ycW4OJgfQQ/playlists
Este curso de Álgebra Abstracta no está en video, sino que es una página html: http://abstract.ups.edu/aata-es/index.html
Álgebra Abstracta y Teoría de Galois
https://www.youtube.com/watch?v=N-5Av1KC11w&list=PLL0ATV5XYF8DTGAPKRPtYa4E8rOLcw88y
Hasta la próxima entrada.
![|G|=|H|[G:H],\,\!](http://upload.wikimedia.org/math/5/5/5/555ef58c070d583f6020601f844966d6.png)
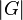 y
y  son el orden del grupo
son el orden del grupo ![[G:H]](http://upload.wikimedia.org/math/8/a/a/8aabaab9682705a6aaca92e78dacbd6f.png) es el
es el
No hay comentarios:
Publicar un comentario
Tu opinión respetuosa con elementales normas de cortesía y convivencia, será siempre bienvenida